วงจรR-L-C (Eng ver.)

RLC Series combinations

Now let's put a resistor, capacitor and inductor in series. At any given time, the voltage across the three components in series, v_series(t), is the sum of these:

v_series(t) = v_R(t) + v_L(t) + v_C(t),

The current i(t) we shall keep sinusoidal, as before. The voltage across the resistor, v_R(t), is in phase with the current. That across the inductor, v_L(t), is 90° ahead and that across the capacitor, v_C(t), is 90° behind.

Once again, the time-dependent voltages v(t) add up at any time, but the RMS voltages V do not simply add up. Once again they can be added by phasors representing the three sinusoidal voltages. Again, let's 'freeze' it in time for the purposes of the addition, which we do in the graphic below. Once more, be careful to distinguish v and V.

Look at the phasor diagram: The voltage across the ideal inductor is antiparallel to that of the capacitor, so the total reactive voltage (the voltage which is 90° ahead of the current) is V_L - V_C, so Pythagoras now gives us:

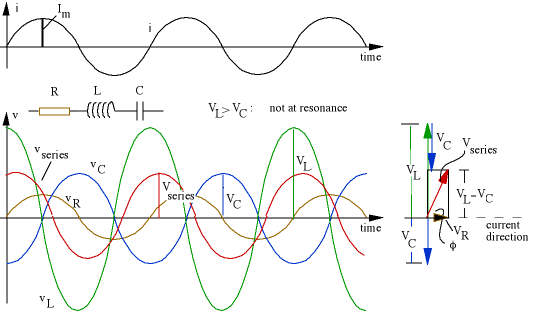
V²_series = V²_R + (V_L - V_C)²

Now V_R = IR, V_L = IX_L = ωL and V_C = IX_C= 1/ωC. Substituting and taking the common factor I gives:

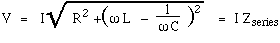
where Z_series is the series impedance: the ratio of the voltage to current in an RLC series ciruit. Note that, once again, reactances and resistances add according to Pythagoras' law:

Z_series² = R² + X_total²
= R² + (X_L- X_C)².

Remember that the inductive and capacitive phasors are 180° out of phase, so their reactances tend to cancel.

Now let's look at the relative phase. The angle by which the voltage leads the current is

φ = tan^-1 ((V_L - V_C)/V_R).

Substiting V_R = IR, V_L = IX_L = ωL and V_C = IX_C= 1/ωC gives:

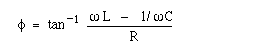
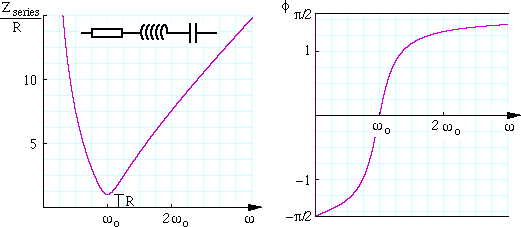
The dependence of Z_series and φ on the angular frequency ω is shown in the next figure. The angular frequency ω is given in terms of a particular value ω_o, the resonant frequency (ω_o² = 1/LC), which we meet below.

(Setting the inductance term to zero gives back the equations we had above for RC circuits, though note that phase is negative, meaning (as we saw above) that voltage lags the current. Similarly, removing the capacitance terms gives the expressions that apply to RL circuits.)

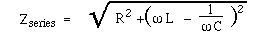
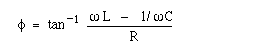
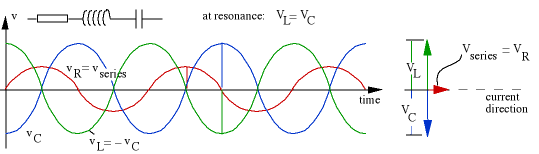
The next graph shows us the special case where the frequency is such that V_L = V_C.

Because v_L(t) and v_C are 180° out of phase, this means that v_L(t) = - v_C(t), so the two reactive voltages cancel out, and the series voltage is just equal to that across the resistor. This case is called series resonance.